
このカリキュラムでは、ニューラルネットワークの学習プロセスにおける重要な概念と手法を体系的に学習します。
基礎的な最適化手法である勾配降下法から、誤差逆伝播の仕組み、活性化関数の種類と特性、さらには特徴学習に活用されるオートエンコーダについて理解を深めます。
1.勾配降下法(Gradient Descent)
ニューラルネットワークの学習において、モデルのパラメータ(重みやバイアス)を適切に調整することは非常に重要です。
そのために用いられるのが 勾配降下法(Gradient Descent) です。
ここでは、勾配降下法の基本概念、損失関数との関係、さらに3つの主要な種類について詳しく解説します。
1.1 勾配降下法とは
パラメータ更新の基本概念
勾配降下法は、損失関数(誤差関数)の値を最小化するために、パラメータ(重み・バイアス)を少しずつ更新していく最適化アルゴリズムです。
ニューラルネットワークの学習では、予測と正解の誤差を最小化するように重みを調整することが求められます。
勾配(Gradient)とは?
勾配とは、関数の傾きを表すベクトルです。
勾配が指し示す方向は、関数が最も急激に増加する方向であり、その逆方向に進めば関数の値を減少させることができます。
勾配降下法の更新式
勾配降下法では、現在のパラメータ θを以下のように更新します。
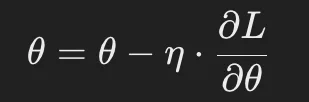
- θ : 更新するパラメータ(重みやバイアス)
- η : 学習率(Learning Rate) – 更新の大きさを決定するハイパーパラメータ
- ∂L/∂θ : 損失関数 Lのパラメータ θに対する勾配
学習率 ηが大きすぎると、最適解を飛び越えてしまい収束しない可能性があります。
逆に、小さすぎると学習が遅くなり、収束までに時間がかかります。
1.2 勾配降下法の種類
1.2.1 バッチ勾配降下法(Batch Gradient Descent)
概要:
バッチ勾配降下法は、訓練データ全体を使って損失関数の勾配を計算し、パラメータを更新する手法です。
更新式:
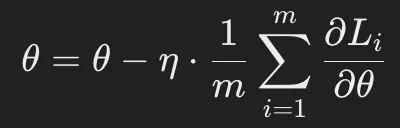
- m : 訓練データ全体のサンプル数
- Li: 各データサンプル iに対する損失関数
メリット:
✅ 勾配の推定が安定しやすい(学習が滑らかに進む)
✅ 最適解への収束が安定する
デメリット:
❌ 訓練データ全体を毎回計算するため、計算コストが高い
❌ 大規模データセットではメモリ不足が発生する可能性がある
適用例:
小規模なデータセットや計算資源に余裕がある場合に適用されることが多い。
1.2.2 確率的勾配降下法(Stochastic Gradient Descent, SGD)
概要:
SGDは、データセットからランダムに選んだ1つのサンプルごとに勾配を計算し、パラメータを更新する手法です。
更新式:
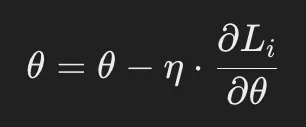
- Li: データサンプルiに対する損失関数
メリット:
✅ 計算コストが低く、大規模データでも処理が可能
✅ 局所最適解に陥りにくく、広い範囲で探索できる
デメリット:
❌ 更新ごとの勾配が不安定で、学習が収束しにくい
❌ 学習率の適切な調整が必要
適用例:
大量のデータを用いたオンライン学習や、計算資源が限られる環境で適用される。
1.2.3 ミニバッチ勾配降下法(Mini-batch Gradient Descent)
概要:
ミニバッチ勾配降下法は、全データを一定サイズの「ミニバッチ」に分け、ミニバッチごとに勾配を計算して更新する手法です。
更新式:
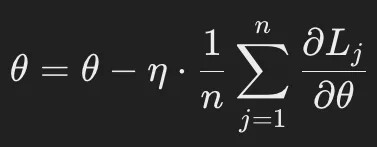
- n : ミニバッチのサイズ
メリット:
✅ SGDよりも収束が安定しやすい
✅ バッチ勾配降下法よりも計算コストを抑えられる
デメリット:
❌ ミニバッチサイズの選定が重要(大きすぎるとメモリ不足、小さすぎると収束が遅くなる)
適用例:
深層学習のトレーニングで一般的に使用される手法で、バッチサイズは 32, 64, 128 などの値がよく採用される。
1.3 勾配降下法の選び方
| 手法 | 計算コスト | 収束の安定性 | 大規模データへの適用 |
|---|---|---|---|
| バッチ勾配降下法 | 高い | 安定 | ❌ メモリ不足の可能性あり |
| 確率的勾配降下法(SGD) | 低い | 不安定 | ◎ 大規模データに向く |
| ミニバッチ勾配降下法 | 中程度 | 比較的安定 | ○ 適用しやすい |
多くのディープラーニングの学習では、ミニバッチ勾配降下法 が最もバランスが良く、主流の手法となっています。
2.誤差逆伝播法(Backpropagation)
ニューラルネットワークの学習では、モデルの予測と正解データとの差(誤差)を最小化することが目的です。
そのためには、各層の重みやバイアスを適切に更新する必要があります。
この更新を効率的に行うために用いられるのが 誤差逆伝播法(Backpropagation) です。
ここでは誤差逆伝播の仕組みを理解し、深層学習の課題である 勾配消失問題 や 局所最適解問題 についても詳しく解説します。
2.1 誤差逆伝播の仕組み
誤差逆伝播法とは?
誤差逆伝播法(Backpropagation)は、ニューラルネットワークの学習時に 勾配を効率的に計算し、各層のパラメータ(重み・バイアス)を更新するアルゴリズム です。
誤差を最小化するために、 チェインルール(連鎖律) を用いて勾配を求めます。
誤差逆伝播の流れ
- 順伝播(Forward Propagation)
- 入力データをニューラルネットワークに通し、各層で活性化関数を適用しながら出力を得る。
- 最終的な出力を使って損失関数の値を計算する。
- 損失関数の計算
- 予測結果と正解データの誤差(損失)を求める。
- 代表的な損失関数:
- 回帰問題 → 平均二乗誤差(MSE)
- 分類問題 → 交差エントロピー誤差(Cross Entropy Loss)
- 逆伝播(Backpropagation)による勾配計算
- 損失関数の値を小さくするため、出力層から入力層に向かって勾配を計算。
- チェインルール(連鎖律) を用いて各層の重みとバイアスの勾配を求める。
- パラメータの更新
- 計算した勾配を使って、勾配降下法(SGDやAdamなど)でパラメータを更新する。
更新式(SGDの例)
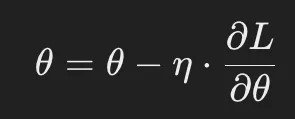
- θ: 更新するパラメータ(重み・バイアス)
- η: 学習率(Learning Rate)
- ∂L/∂θ: 損失関数 Lの勾配
2.2 勾配消失問題とその対策
勾配消失問題とは?
深いニューラルネットワークでは、誤差逆伝播の際に 層を遡るほど勾配が小さくなり、学習が進まなくなる ことがあります。
特に シグモイド関数やTanh関数 を活性化関数に用いた場合、勾配が小さくなりやすいです。
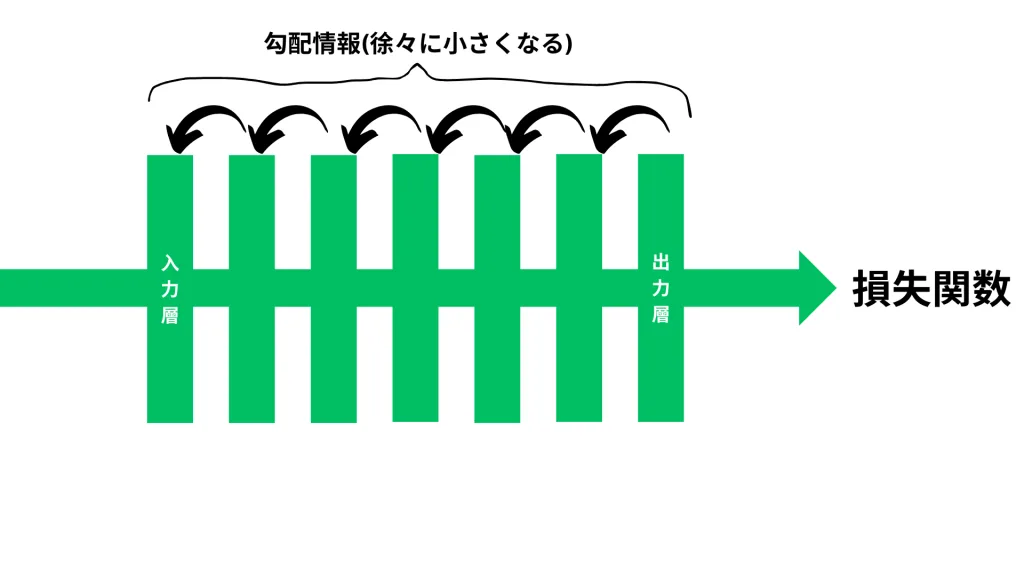
なぜ勾配が消失するのか?
誤差逆伝播では、チェインルールにより層ごとに勾配を掛け合わせて計算します。
例えば、シグモイド関数の微分は最大でも 0.25 であり、多層のネットワークでは勾配が 0 に近づいてしまう ため、学習が進まなくなります。
勾配消失問題の対策
① 活性化関数の工夫(ReLUの使用)
- ReLU(Rectified Linear Unit)関数 を活性化関数として使用することで、勾配消失問題を軽減できます。
- ReLUの定義:
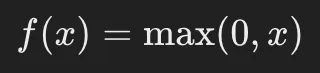
- 勾配は 1 または 0 となるため、層を遡っても勾配が極端に小さくなることがありません。
② 重みの適切な初期化(Xavier, He 初期化)
- 重みの初期値が不適切だと、学習初期の段階で勾配が小さくなりやすい。
- Xavier初期化(Glorot Initialization)
- シグモイドやTanh関数を使う場合に適した重みの初期化手法。
- He初期化(He Initialization)
- ReLUを使う場合に適した初期化手法。
③ バッチ正規化(Batch Normalization)
- 各層の出力を正規化することで、勾配のスケールを適切に保つ手法。
- 学習が安定し、勾配消失の影響を抑えられる。
2.3 局所最適解問題とその回避策
局所最適解とは?
ニューラルネットワークの学習では、損失関数の最適解に到達しようとしますが、
全体で最も良い グローバル最適解(Global Optimum) ではなく、途中の 局所最適解(Local Optimum) に陥る場合があります。
なぜ局所最適解に陥るのか?
- 勾配降下法は、現在の勾配が小さい方向にパラメータを更新するため、局所最適解に捕まる可能性がある。
- ニューラルネットワークの損失関数は高次元空間であり、多くの局所的な谷が存在する。
局所最適解の回避策
① モーメンタム(Momentum)の導入
- 過去の勾配の移動方向を考慮し、慣性を持たせることで局所最適解を脱出しやすくする。
- 更新式:
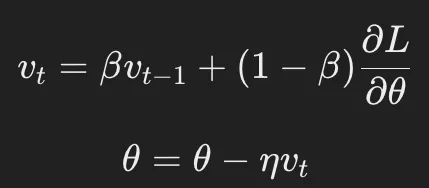
- βは慣性の強さを決めるハイパーパラメータ(一般的に 0.9 などを使用)。
② Adamオプティマイザの活用
- 勾配の移動平均(モーメンタム)と、勾配の2乗の移動平均を組み合わせた最適化手法。
- 学習率の調整が自動で行われ、局所最適解を回避しやすい。
③ 初期値のランダム化
- 重みの初期値をランダムに設定することで、異なる局所最適解に収束しにくくなる。
- 複数の異なる初期値で学習を試す ことも有効。
3.活性化関数(Activation Functions)
ニューラルネットワークの各層では、活性化関数(Activation Function) を使用して、入力データを変換し、次の層に伝える重要な役割を果たします。
適切な活性化関数を選択することで、ネットワークの学習速度や精度が向上し、勾配消失問題などの課題を軽減できます。
ここでは、主要な活性化関数 (シグモイド関数、Tanh関数、ReLU関数、ソフトマックス関数) について詳しく解説します。
3.1 シグモイド関数(Sigmoid Function)
定義
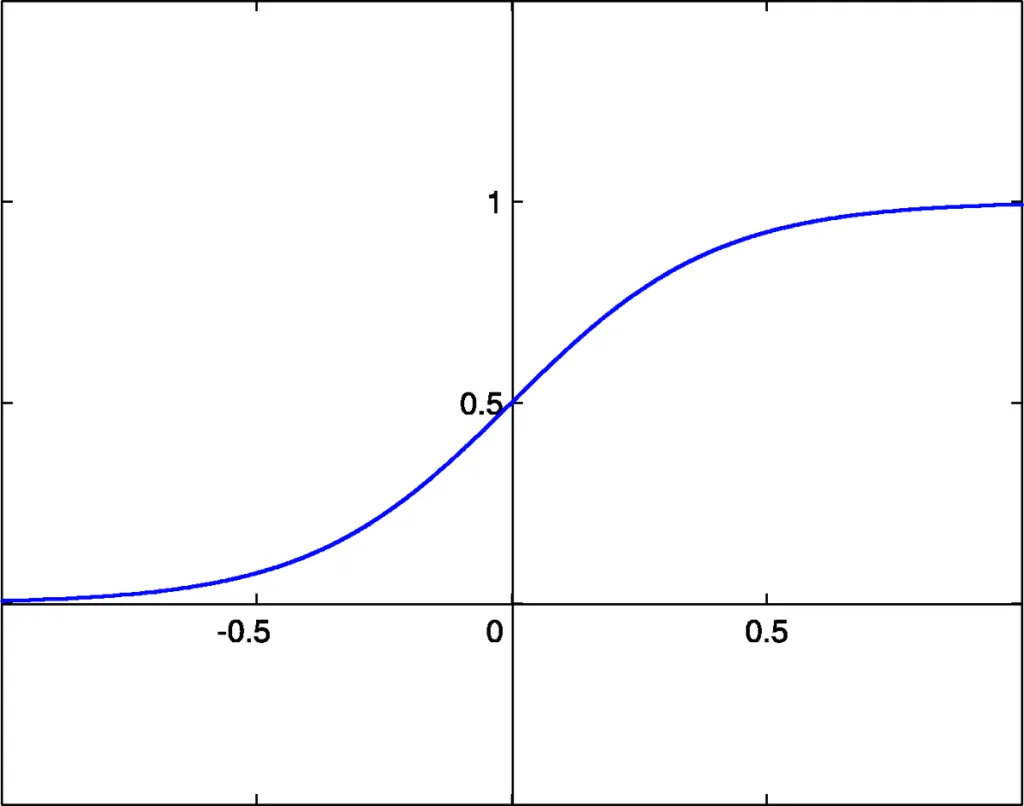
シグモイド関数は、入力値を0から1の範囲に変換する活性化関数です。
以下の式で定義されます。
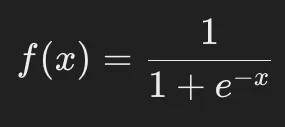
特徴
✅ 出力が0から1の範囲に収まる
- 出力が確率のように解釈できるため、2値分類問題に適している。
✅ 非線形性を持つ
- 線形関数では表現できない複雑な関係を学習可能。
❌ 勾配消失問題が発生しやすい
- シグモイド関数の勾配は、極端な値(非常に大きい or 小さい x)では 0 に近づく。
- そのため、逆伝播の際に 勾配が小さくなりすぎて学習が進まない(勾配消失問題) が発生する。
❌ 出力の中心が0ではない(非対称)
- 出力が 常に正(0〜1の範囲) のため、勾配の平均値がゼロに近づきにくい。
- その結果、学習の効率が低下することがある。
適用例
- ロジスティック回帰(Logistic Regression)
- 2クラス分類問題の出力層
- 例:画像分類(猫 or 犬など)
3.2 Tanh関数(Hyperbolic Tangent Function)
定義
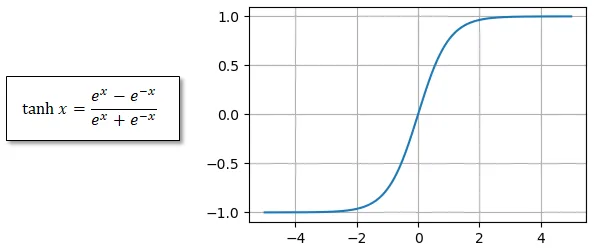
Tanh関数(双曲線正接関数)は、-1から1の範囲に出力をスケーリングする活性化関数です。
以下の式で定義されます。
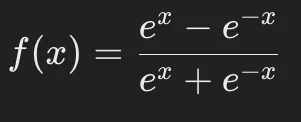
特徴
✅ 出力が-1から1の範囲に収まる(中心が0)
- シグモイド関数と異なり、出力が 負の値を取る ため、学習時の重みの変化が対称的になりやすい。
- その結果、学習が 効率的に進みやすい。
✅ シグモイド関数より勾配消失問題が起こりにくい
- 勾配の最大値が 1 であり、シグモイドより情報の流れを維持しやすい。
❌ 極端な値では勾配消失が発生する
- xが大きすぎる(または小さすぎる)と、勾配が 0 に近づき、学習が停滞する。
適用例
- 隠れ層の活性化関数(シグモイドの代替として使用)
- 自然言語処理(RNNの活性化関数として利用されることが多い)
3.3 ReLU関数(Rectified Linear Unit Function)
定義
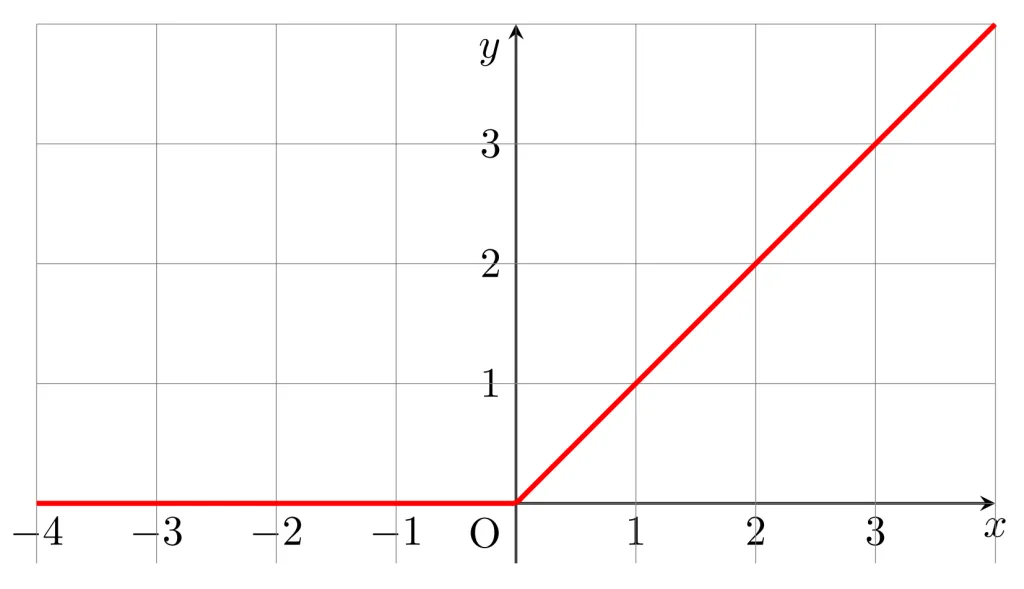
ReLU(Rectified Linear Unit)関数は、入力が 0以下の場合は0、0より大きい場合はそのまま出力する シンプルな活性化関数です。
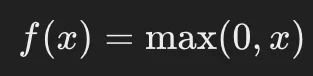
特徴
✅ 勾配消失問題を軽減できる
- シグモイドやTanhのように勾配が小さくならず、学習を加速できる。
✅ 計算がシンプルで効率的
- 乗算や指数演算が不要なため、高速な計算が可能。
❌ 「死んだニューロン(Dead Neuron)」問題
- 入力が負の値のとき、勾配が 0 になるため、そのニューロンは学習に寄与しなくなる。
- これが続くと、ネットワークの一部が機能しなくなる可能性がある。
改良版 ReLU の紹介
- Leaky ReLU:
- 負の値のときも微小な値を出力する(例:f(x)=0.01x for x<0)。
- 死んだニューロンを防ぐために開発された。
- Parametric ReLU(PReLU):
- 負の部分のスケールを学習可能なパラメータとして調整できる。
適用例
- CNN(畳み込みニューラルネットワーク)
- DNN(深層学習の隠れ層)
- 一般的な深層ニューラルネットワーク全般
3.4 ソフトマックス関数(Softmax Function)
定義
ソフトマックス関数は、多クラス分類問題の出力層でよく使われる活性化関数で、各クラスの確率を計算する ために使用されます。
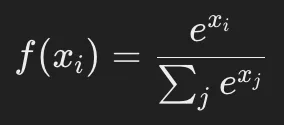
ここで:
- xiは出力層のニューロンのスコア(ロジット)
- 分母の合計値はすべてのクラスの指数関数の和
特徴
✅ 出力が確率分布になる
- すべての出力値の合計が 1 になるため、確率として解釈できる。
✅ 多クラス分類に適している
- 各クラスのスコアを適切にスケーリングし、確率として扱えるようにする。
❌ 大きな値が支配的になりやすい
- ロジットの値が大きい場合、1つのクラスが圧倒的に支配的になり、学習が偏る可能性がある。
- その対策として、ソフトマックスとともに交差エントロピー損失(Cross Entropy Loss)を使用する ことが一般的。
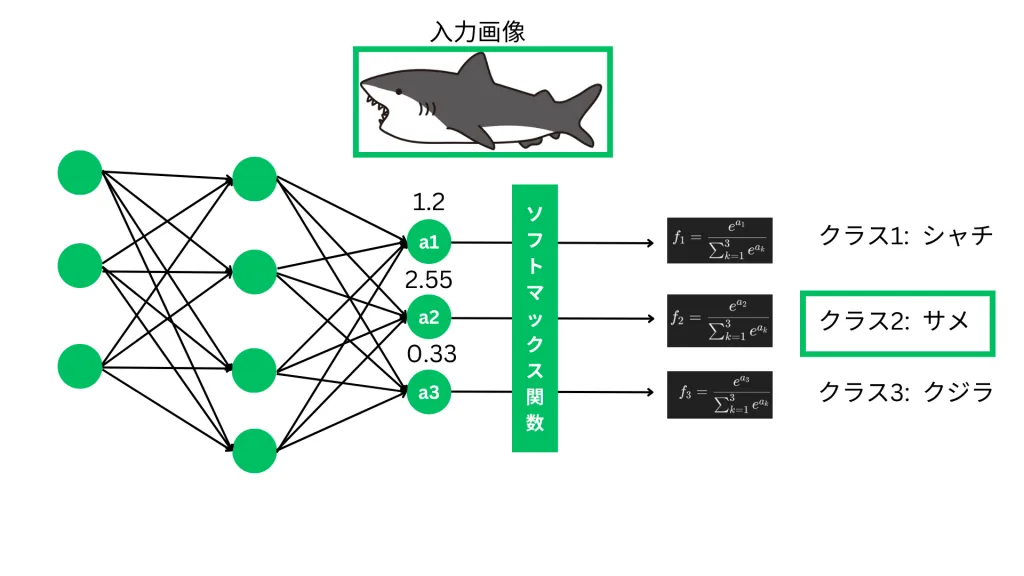
適用例
- 多クラス分類の出力層(例:画像認識での猫・犬・鳥の分類)
- 自然言語処理(単語の確率分布を求める際に使用)
4.オートエンコーダ(Autoencoder)
オートエンコーダ(Autoencoder)は、入力データを圧縮(エンコード)し、それを再構成(デコード)するニューラルネットワーク です。
このネットワークは教師なし学習に分類され、特徴抽出、異常検知、次元削減 などに広く活用されています。
ここでは、オートエンコーダの概要、ネットワーク構成、代表的な応用例について詳しく解説します。
4.1 オートエンコーダの概要
オートエンコーダとは?
オートエンコーダは、入力データを低次元の潜在空間(Latent Space)に圧縮し、元のデータを再構成する ニューラルネットワークの一種です。
このプロセスにより、データの重要な特徴を抽出し、不要な情報を削減することが可能になります。
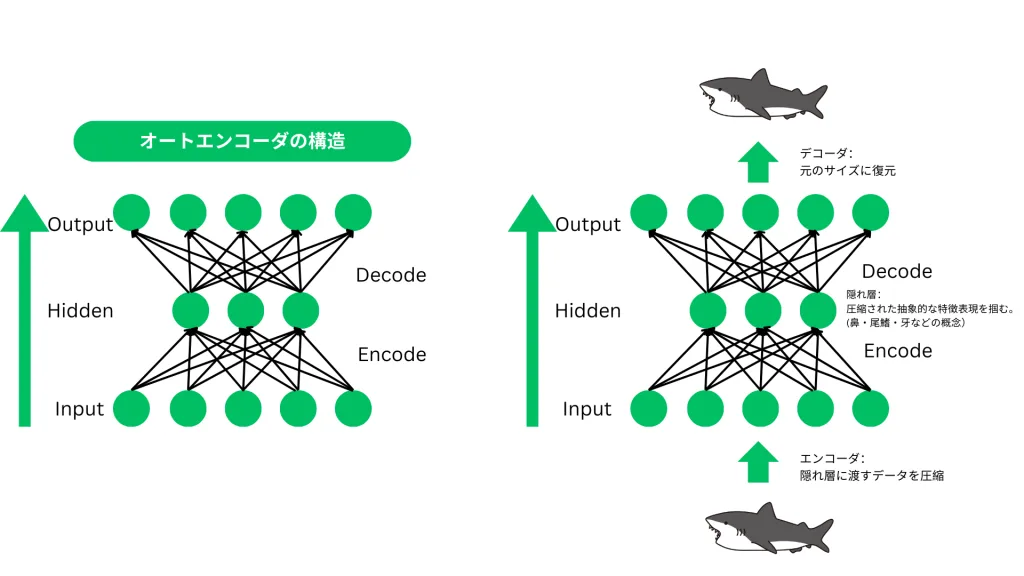
オートエンコーダの基本的な学習プロセス
- エンコーダ(Encoder)
- 入力データ Xを低次元の特徴ベクトル Zに変換する。
- この変換により、データの重要な特徴を圧縮し、次元削減が可能になる。
- 例:高解像度の画像を小さな特徴マップに変換。
- 潜在空間(Latent Space)
- 圧縮されたデータの表現(特徴量)を持つ空間。
- ここで、データの構造を学習し、新しい特徴を発見することができる。
- デコーダ(Decoder)
- エンコーダが作成した特徴ベクトル Zから元の入力データ X′を再構成する。
- もし再構成がうまくいけば、エンコーダがデータの本質的な特徴を適切に学習できたことになる。
オートエンコーダの学習方法
オートエンコーダの学習は、入力データ XXX をそのまま ターゲットデータ として使用し、出力 X′と Xの誤差(損失関数)を最小化する ように行われます。
一般的な損失関数:
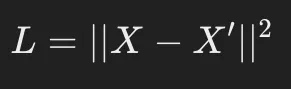
(元のデータ Xと再構成データ X′の二乗誤差を最小化する)
4.2 オートエンコーダの構成
オートエンコーダは、大きく分けて エンコーダ(Encoder) と デコーダ(Decoder) の2つのネットワークから構成されます。
4.2.1 エンコーダ(Encoder)
- 役割: 入力データを圧縮し、低次元の潜在空間(Latent Space)に変換する。
- 仕組み:
- 複数の 全結合層(Fully Connected Layer) または 畳み込み層(Convolutional Layer) を使用。
- 活性化関数には ReLU や シグモイド関数 などが用いられる。
- 入力次元 Dを小さな次元 d(d<Dd) に圧縮する。
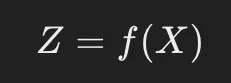
X(入力データ) → エンコーダ → Z(圧縮されたデータ)
4.2.2 デコーダ(Decoder)
- 役割: 圧縮されたデータを元のデータに復元する。
- 仕組み:
- エンコーダと対称な構造を持ち、圧縮された特徴ベクトル ZZZ から入力データ X′X’X′ を再構成する。
- 全結合層(FC層) または 転置畳み込み層(Transposed Convolution) を使用。
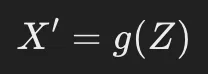
Z(圧縮データ) → デコーダ → X′(再構成データ)
4.2.3 損失関数と最適化
オートエンコーダの学習では、元の入力データ X と再構成された出力データ X′ の誤差を最小化する ように学習が進められます。
代表的な損失関数:
- MSE(Mean Squared Error):
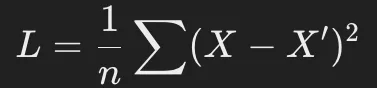
- クロスエントロピー損失(Binary Cross-Entropy Loss):
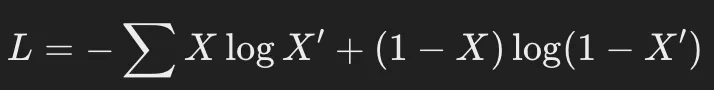
4.3 オートエンコーダの応用例
オートエンコーダは、特徴抽出や異常検知など、さまざまな分野で活用されています。
ここでは、代表的な3つの応用例について紹介します。
4.3.1 画像のノイズ除去(Denoising Autoencoder)
概要:
- 画像にノイズを加えたデータを入力し、オートエンコーダを用いてノイズを取り除く。
- 正しい特徴を学習することで、画像のノイズを除去(Denoising) することが可能。
仕組み:
- ノイズ付き画像 Xnoisyをエンコーダに入力。
- エンコーダが特徴を抽出し、潜在空間へ変換。
- デコーダが元のクリーンな画像 XcleanX_{clean}Xclean を復元。
- 損失関数を用いて、元画像と出力の誤差を最小化するように学習。
応用例:
- MRIやX線画像のノイズ除去
- 古い写真の修復
4.3.2 異常検知(Anomaly Detection)
概要:
- 通常データを用いてオートエンコーダを学習し、異常データを検出する。
- 異常データは再構成誤差が大きくなる ため、それを指標に異常を識別。
仕組み:
- 正常なデータのみを用いてオートエンコーダを学習。
- 新しいデータを入力し、再構成誤差を計算。
- 再構成誤差が大きい場合、それを異常と判定。
応用例:
- クレジットカードの不正利用検出
- 製造業の異常検知(欠陥品の発見)
4.3.3 次元削減(Dimensionality Reduction)
概要:
- 高次元データを圧縮し、情報を失わずに低次元表現に変換する。
- PCA(主成分分析)よりも 非線形なデータ構造を捉えられる ため、高精度な次元削減が可能。
応用例:
- 大量の特徴量を持つデータの可視化
- 画像・音声データの圧縮
まとめ
本カリキュラムでは、ニューラルネットワークの学習プロセスを理解するために、勾配降下法や誤差逆伝播法、各種活性化関数、オートエンコーダについて学習しました。
ニューラルネットワークのパフォーマンスを向上させるには、最適化手法の選択や活性化関数の適用が重要です。



