機械学習の分野では、ニューラルネットワークが数多くの問題を解決する万能ツールとして知られています。
しかし、ニューラルネットワークの背後にある理論的基盤について深く掘り下げると、その一つに「コルモゴロフ・アーノルド表現定理」があります。
この定理は、任意の連続関数を複数の一変数関数の組み合わせで表現できることを示しています。
この記事では、この定理を基に構築された新世代のニューラルネットワークである「Kolmogorov arnold network(KAN)」について詳しく解説します。
1.KANとは?
KAN(Kolmogorov-Arnold Networks) は2024年4月30日arXivに投稿された論文にて提案された新たなニューラルネットワークのことを指します。
コルモゴロフ・アーノルド表現定理(Kolmogorov-Arnold representation theorem)に基づいて設計されており、非線形な活性化関数そのものを直接学習することから、パラメータ効率が良く、学習結果の解釈可能性が高いことが特徴です。
2.従来のMLP VS KAN
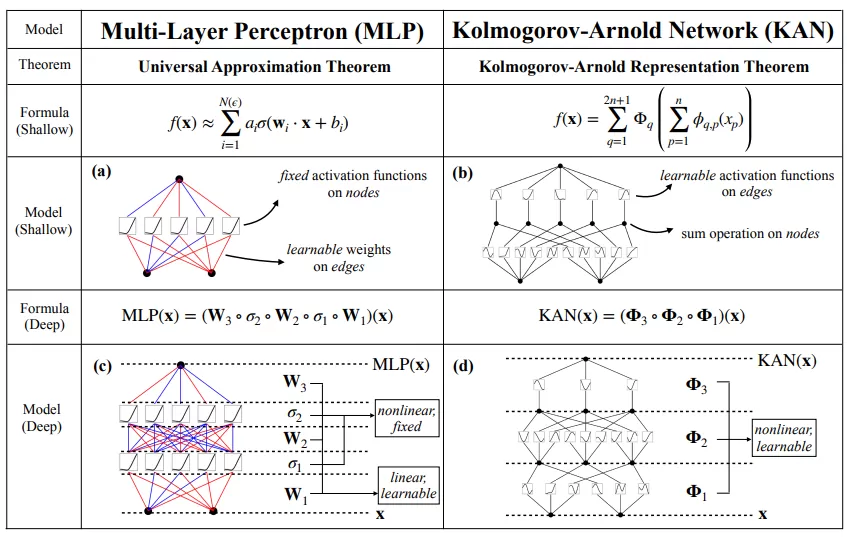
MLPとKANの違いは上の図のに詳しく示されていますが、ここではその主な違いを以下に説明します。
MLP(多層パーセプトロン)
- ノード:各エッジからの入力に対し、事前に定義された非線形変換を適用し、これを学習することはできません。その後、変換された結果を全て合計して次のエッジに送ります。
- エッジ:各ノードからの入力に対して、学習可能なパラメータを使用した線形変換を行い、その結果を次のノードに送ります。
KAN(Kolmogorov–Arnold Network)
- ノード:複数のエッジからの入力を合計し、その結果を次のエッジに伝えます。
- エッジ:各ノードからの入力に、学習可能なパラメータを用いた非線形変換を適用し、結果を次のノードに送ります。
ここで強調したいのは、「学習可能/学習不可能」および「非線形変換/線形変換」という概念です。
MLPではこれらの特徴が混在していましたが、KANでは強みのみを活かすことで構造が簡素化されており、特に深層学習の分野で懸念されるパラメータの増加を抑えることが可能です。
また、KANはMLPに比べてモデルの解釈性が高くなっています。
変換の内容はMLPよりも複雑ですが、KANの各変換はより直接的で明確な表現を行うことができ、その分変換回数も少なく済むのです。
KANの現時点での欠点
公平に述べるならば、KANは同じパラメータ数を持つMLPと比べて訓練時間が長くなりがちです。
したがって、迅速な訓練が求められる場合にはMLPの方が適している場合があります。
ただし、KANの計算時間に関する研究はまだ進行中であり、今後の最適化により改善される可能性は十分にあります。
KANのメリットとデメリットのまとめ
メリット
- パラメータの効率化による削減が可能
- モデルの解釈性が向上
デメリット
- 訓練に時間がかかる
3.コルモゴロフ・アーノルド表現定理とは?
コルモゴロフ・アーノルド表現定理は、任意の連続関数を複数の一変数関数で表現できるという強力な数学的結果です。
具体的には、任意の n 変数連続関数 f(x1, x2, …, xn) が、次の形で表現できることを保証します
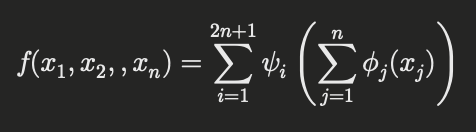
ここで、ψiや φjは一変数関数であり、この構造により高次元の関数もシンプルな構成で表現可能となります。
定理の意義
この表現は、次の2つの重要な点で意義を持っています:
1. 高次元問題の単純化
多変数関数を取り扱う際、従来は多次元の空間を直接処理する必要がありました。
しかし、コルモゴロフ・アーノルド表現定理を用いることで、元の高次元関数を複数の一変数関数の組み合わせに分解できます。
これにより、計算の複雑さが大幅に減少し、問題が単純化されます。
2. ニューラルネットワークへの応用
この定理が重要なのは、単に数学的な興味だけではありません。
特に、ニューラルネットワークにおいて、コルモゴロフ・アーノルド表現定理は普遍的近似性能の理論的基盤となっています。
すなわち、ニューラルネットワークが任意の複雑な関数を近似する能力を持っている理由の一つが、この表現定理にあります。
数式の解釈
定理の式において、以下のような解釈が可能です:
- f(x1, x2, …, xn) は、多変数の関数。たとえば、3変数 x1, x2, x3 を持つ関数 f(x1, x2, x3) として考えることができる。
- ψi は一変数関数で、複数の ψi が存在し、それぞれがある変換を担当する。
- φj(xj) も一変数関数で、それぞれの変数φj を別々に処理する。
式の構造を見ると、各変数 xj に対して一変数関数 φj(xj) を適用し、それらを合計した後、さらに別の一変数関数ψi を適用して最終的な出力を得ることがわかります。
これは、複雑な関数をシンプルな処理に分解する有効な方法です。
4.Kolmogorov–Arnold Network(KAN)の仕組み
コルモゴロフ・アーノルドネットワークは、既存のニューラルネットワーク(特に多層パーセプトロン:MLP)とは異なる独自のアプローチで関数近似を行います。
このネットワークの基盤は「コルモゴロフ・アーノルド表現定理」にあり、この定理によって、多変数関数をシンプルな一変数関数に分解し、効率的に表現・学習できる仕組みが提供されます。
従来のMLPは、全ての入力変数に対して重みとバイアスを使って線形変換を行い、その後活性化関数を用いて非線形変換を施します。
しかし、コルモゴロフ・アーノルドネットワークでは、入力を個別の一変数関数に分解し、それぞれを別々に処理した後、結果を組み合わせます。
これによって、計算効率が向上し、より少ないパラメータで同等の精度を実現することができます。
1.一変数関数への分解
このネットワークの最初のステップは、入力データをそれぞれの変数ごとに一変数関数に分解することです。
通常のニューラルネットワークでは、全ての入力変数を一括して処理しますが、コルモゴロフ・アーノルドネットワークでは、次のように各変数を個別に処理します。
例えば、入力データが 3次元の (x1, x2, x3) であった場合、各次元に対して異なる一変数関数 φ1(x1), φ2(x2), φ3(x3) を適用します。
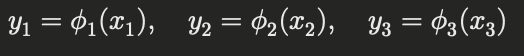
この段階では、各変数ごとに非線形な変換が行われます。この変換により、データの特徴を抽出し、個別に処理することで複雑なデータ構造を簡潔に扱うことができます。
2.内部での合成
次に、変数ごとに処理された結果 y1, y2, y3 を組み合わせて最終的な出力を得ます。
ここでの特徴は、複数の一変数関数ψi を用いて、合成する際に非線形な組み合わせが行われる点です。
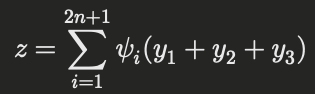
この手法では、単に値を足し合わせるだけではなく、それらに対して別の一変数関数を適用することで、元の複雑な多変数関数を再現します。重要なのは、このプロセスが多層ニューラルネットワークのように層を重ねなくても、複雑な関数を近似できるということです。
コルモゴロフ・アーノルドネットワークのアプローチでは、多層ネットワークのパラメータ数が増加する問題を回避でき、計算コストが低減されます。通常のニューラルネットワークでは、多層化することで学習の精度が向上する反面、過学習や計算リソースの増加といった課題が発生しますが、このネットワークではそのような問題を軽減できます。
3.出力の生成
最終的に、合成された値 z がネットワークの出力として得られます。
この出力は、複数の入力変数が個別に処理され、非線形に組み合わせられた結果として、高次元のデータに対する複雑な関数を効率的に表現しています。
これにより、少ないパラメータで高精度な関数近似が実現可能です。
コルモゴロフ・アーノルドネットワークは、ニューラルネットワークの理論的基盤である「普遍的近似性能」を保ちながら、効率的にデータの複雑なパターンを学習できる点が特徴です。
コルモゴロフ・アーノルドネットワークの強み
コルモゴロフ・アーノルドネットワークの最大の強みは、少ないパラメータで複雑な関数を高精度で近似できることです。
これは、従来のニューラルネットワークと比較して、以下の利点を持ちます:
- パラメータ数の削減:通常のMLPでは、各層で大量の重みやバイアスが必要ですが、コルモゴロフ・アーノルドネットワークでは、一変数関数に分解することで必要なパラメータ数を大幅に削減できます。これにより、学習の効率が向上し、計算コストを削減できます。
- 過学習のリスク軽減:ネットワークが複雑になると、過学習(トレーニングデータに過度に適合することで、未知のデータに対して精度が低下する現象)が問題となりますが、コルモゴロフ・アーノルドネットワークでは、適切に関数を分解・合成することで、過学習のリスクを抑えつつ、高精度な近似が可能です。
- 計算効率の向上:多層ニューラルネットワークでは、層が増えるごとに計算コストが上昇しますが、コルモゴロフ・アーノルドネットワークでは、層を重ねることなく複雑な関数を近似できるため、効率的な学習と推論が可能です。特に、高次元データを扱うタスクにおいては、この効率性が大きな利点となります。
5.応用の可能性
コルモゴロフ・アーノルドネットワークは、その理論的な強さと効率性から、さまざまな実世界の問題に適用することができます。
特に、複雑な多変数関数の学習が必要とされる分野で、その性能が際立ちます。
以下では、代表的な応用分野とその理由について詳しく説明します。
1. 時系列予測
時系列予測では、過去のデータから未来の動きを予測するため、多くの場合、複数の変数が時間とともに変動します。
特に、多変量時系列データでは、複数の要素が相互に依存し合うため、その関係を正確にモデリングすることが非常に重要です。
従来の課題
従来のMLPや他のニューラルネットワークでは、多くの変数を扱う時にパラメータの数が膨大になりがちで、その結果、学習に時間がかかり、過学習のリスクも増します。
また、時系列データの特性である「時点間の相関関係」をしっかりと捉えるために、ネットワークの深さを増やす必要があり、これがさらに計算負荷を増大させます。
コルモゴロフ・アーノルドネットワークの強み
コルモゴロフ・アーノルドネットワークは、まず多変数を個々の一変数関数に分解して処理するため、複数の時系列データを効率的に学習できます。
ネットワークのパラメータ数が少ないため、時系列データの時間的依存関係を過度に複雑にすることなく、正確にモデル化できます。
また、少数のパラメータで高次元データを扱うため、トレーニング速度も従来の手法に比べて速く、予測精度も維持されます。
実際の応用例
例えば、株式市場や為替市場など、経済や金融の時系列データの予測にコルモゴロフ・アーノルドネットワークが応用されることが考えられます。
市場データは複数の要因(価格、出来高、金利、経済指標など)が絡み合い、時間とともに複雑な動きを見せますが、このような高次元のデータを効果的にモデル化し、未来の動きを予測するツールとして利用できます。
2. 画像認識
画像認識は、コンピュータビジョン分野において最も重要なタスクの一つで、通常、画像は非常に高次元のデータです。
各ピクセルが特徴ベクトルとして扱われ、何百万というデータポイントが存在するため、その全てを効率的に学習するためには強力なモデルが必要です。
従来の課題
従来の画像認識タスクでは、畳み込みニューラルネットワーク(CNN)が主流となっていますが、これらは大規模なデータセットに依存し、計算負荷も高くなりがちです。
特に、画像データの高次元性に伴うパラメータの増加が問題となります。
さらに、CNNでは画像全体をフィルターを通して処理するため、局所的な特徴に注目しますが、全体の構造を効率よく扱うことは難しい場合があります。
コルモゴロフ・アーノルドネットワークの強み
コルモゴロフ・アーノルドネットワークでは、画像のピクセルごとの特徴を一変数関数として分解し、それらを非線形に合成して出力を生成します。
これにより、各ピクセル間の関係をシンプルかつ効率的に表現でき、CNNと同等の性能をより少ないパラメータで実現可能です。
また、ネットワークの構造が軽量であるため、大規模なデータセットに対しても迅速に学習が進む点が大きな強みです。
実際の応用例
医療画像の解析において、特にMRIやCTスキャンのような高解像度画像の認識に使用できます。
これらのデータは非常に高次元であり、従来の手法では計算コストが高いため、コルモゴロフ・アーノルドネットワークを使うことで、早期の病変発見や診断を効率的に行うことが可能になります。
3. 金融データのモデリング
金融データのモデリングは、ポートフォリオの最適化、リスク管理、価格予測など、幅広い分野で重要な役割を果たしています。
金融データは多次元で、各変数が相互に影響を与える複雑な構造を持っています。
株価や為替レート、経済指標、企業の財務情報など、変数の相関を正確にモデリングすることが求められます。
従来の課題
金融データのモデリングにおいては、多変数の依存関係を正確に捉えるために、多層のネットワークが必要とされることが一般的です。
MLPを用いた場合、金融データの多次元性と相関関係を学習するためには、膨大な数のパラメータを必要とし、学習に時間がかかる上、過学習のリスクも高まります。
コルモゴロフ・アーノルドネットワークの強み
コルモゴロフ・アーノルドネットワークは、金融データの多次元性に対して、個別の変数を一変数関数に分解し、それらを効率的に処理することができます。
これにより、従来の手法に比べてパラメータ数が少なく、効率的に学習を進めることが可能です。
また、金融データのような複雑な依存関係も非線形な合成を通じて捉えることができ、リスク管理や投資戦略の最適化に役立ちます。
実際の応用例
リスク管理の分野で、コルモゴロフ・アーノルドネットワークは、クレジットリスクや市場リスクのモデリングに適用されることが考えられます。
特に、多くの変数(例えば、金利、為替レート、信用スプレッドなど)が絡むシステムの中で、効率的にリスクの評価を行うことが可能です。
さらに、金融機関における不正取引の検出や、フィンテック企業によるローン申請の審査など、幅広い分野での応用が期待されています。
まとめ
コルモゴロフ・アーノルドネットワークは、従来のニューラルネットワークアーキテクチャとは一線を画し、数学的に強力な基盤に基づいて効率的な関数近似を実現します。処理スピードにまだまだ課題はあるものの、高次元データの処理において、少ないパラメータで複雑な関数の表現が可能であるため、さまざまな応用分野で今後の展開が期待されています。



