はじめに
どうもエンジニアのKです。
今回は、AI開発において必需品とも言える「最適化アルゴリズム」について、ブログにしてみました。
普段AI開発をしていると、深い理解もせずに使ってしまいがちな「最適化アルゴリズム」ですが、実際は多くの種類があり、状況に応じて使い分ける能力が必要になってきます。
このブログで、「最適化アルゴリズム」についての理解を深め、AI開発のレベルを一段階あげてみましょう。
1. オプティマイザの基本
オプティマイザは、機械学習のトレーニングプロセスにおいて、目的関数の最適化を通じて最良のモデルパラメータを特定するためのアルゴリズムです。
ここでは、その理論的背景と数学的定式化について掘り下げます。
勾配降下法（Gradient Descent）
このアルゴリズムは最も基本的な形式であり、パラメータ空間において損失関数の勾配が指し示す方向に逆らってパラメータを更新することで局所最小値を探求します。
数学的には、以下の更新規則に従います：
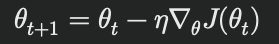
ここで、θはパラメータ、ηは学習率、 J は損失関数、∇θJ(θt) はθにおける損失関数の勾配です。
この手法はシンプルである一方、学習率の選択や局所最適解への収束が主要な課題となります。
確率的勾配降下法（Stochastic Gradient Descent, SGD）
SGDは、勾配降下法の計算効率を改善したバリエーションで、全データセットではなくランダムに選ばれたサンプルを用いて勾配を計算します。
これにより、更新がより頻繁に行われ、大規模データセットに適用可能です。
数学的には次のように表されます：
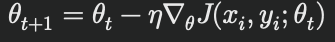
ここで、( (xi, yi) ) はランダムに選ばれた訓練データのサンプルです。
SGDは非凸条件下での収束性に優れ、局所最適解に陥るリスクを減少させる可能性がありますが、ノイズが多いため、より洗練された変種が提案されています。
この最適化アルゴリズムは、AI開発において一番よく使われる手法にもなっています。
モーメンタム
モーメンタム手法は、物理学における運動量の概念に着想を得ており、勾配の過去の蓄積（モーメンタム）を利用してパラメータの更新を行います。
これにより、局所最適解の問題を緩和し、収束を加速させることができます。
更新式は以下の通りです：
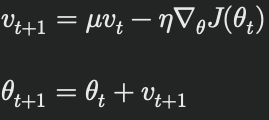
ここで、vtは時刻 t におけるパラメータの更新ベクトル、μはモーメンタム係数です。
アダム（Adaptive Moment Estimation）
アダムはモーメンタムと適応的な学習率を組み合わせたオプティマイザで、各パラメータに対して個別の学習率を調整します。
この手法は、特に非凸最適化問題において高い性能を示します。
アダムの更新式は以下の通りです：
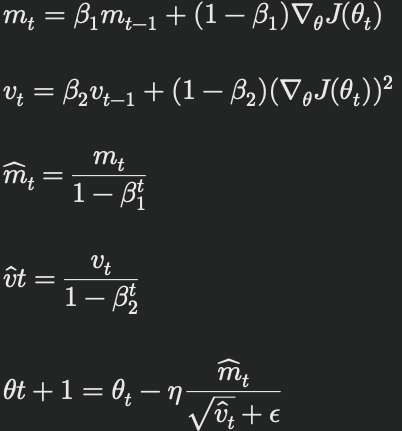
ここで、mtとvtはそれぞれ一次と二次のモーメント推定値、β1とβ2 は減衰率、εは数値安定性のための小さな定数です。
これらの進歩的なアプローチにより、機械学習のトレーニングプロセスはより効率的かつ効果的になり、複雑なデータセットとモデルアーキテクチャに対応する能力が向上しています。
2.局所最適解と非凸最適化問題
非凸最適化問題とは
非凸最適化問題は、損失関数が複雑で多数の局所最小値や鞍点、広い平坦な領域を含むことが特徴です。
これらの特性は、特にディープニューラルネットワークのような大規模モデルにおいて顕著で、損失関数が非凸であるために、全体の最小値を見つけるための探索が困難になります。
非凸性はアルゴリズムが全体の最小値に到達することを困難にし、局所的な最小値に収束することが多いです。
非凸最適化問題では、目的関数（または損失関数）が非凸性を示します。これは、関数が一つのグローバル最適解ではなく、複数の局所最適解を持つ可能性があることを意味します。非凸関数は通常、以下の特性を持ちます：
• 複数の局所最適解：関数は一つ以上の局所的な最低点を持ちます。
• 鞍点：これらは局所最小値でも最大値でもないが、ある方向では最小値、別の方向では最大値となる点です。
• 非連続点：関数が急激に変化する点や、導関数が存在しない点も含まれます。
非凸最適化の課題
非凸最適化問題の主な課題は、真のグローバル最適解を見つけることが非常に困難であることです。これは次の理由によります：
• 局所最適解の存在：アルゴリズムが局所最適解に収束しやすく、これがグローバル最適解かどうかを判断することが難しい。
• 探索空間の広さ：高次元空間では、探索すべき領域が非常に広大になり、効率的な探索が困難になります。
• 鞍点の多数存在：鞍点はしばしば局所最適解と誤認され、最適化プロセスを停滞させる原因となります。
局所最適解とは
定義と特徴：
局所最適解は、損失関数の定義域の部分集合において最小値を取る点です。
この部分集合内では、その点よりも小さい値の損失を持つ他の点は存在しませんが、定義域全体を考慮すると、より低い損失を持つ別の点（グローバル最適解）が存在する可能性があります。
局所最適解は、損失関数の地形が複雑で多くの凹凸がある場合にしばしば発生します。
発生する背景：
高次元のパラメータ空間や非凸損失関数を持つディープラーニングモデルでは、多数の局所最適解が生成されることが一般的です。
これは、ネットワークのアーキテクチャ、特に深い隠れ層や非線形活性化関数の使用により、損失面が複雑化されるためです。
局所最適解の影響
局所最適解に収束することは、モデルの性能に様々な影響を及ぼす可能性があります。
最も顕著なのは、モデルがデータに過剰に適合し、新しいデータや異なるデータ分布に対する一般化能力が低下することです。
また、局所最適解はしばしば、学習プロセスの効率を低下させ、必要なトレーニング時間を増加させます。
局所最適解と鞍点の関係
局所最適解に加えて、鞍点も非凸最適化問題における重要な現象です。
鞍点は、いくつかの次元では勾配が正、他の次元では勾配が負になる点であり、これらの点が局所最適解かどうかを判定するのが難しいことがあります。
現代の最適化アルゴリズムでは、これらの鞍点を効率的に越えることが重要な課題とされています。
非凸最適化のアプローチ
非凸問題に対処するためのいくつかの一般的なアプローチは以下の通りです：
1. 勾配ベースの手法：
• 確率的勾配降下法（SGD）：ランダムなサンプルを使用して勾配を推定し、局所最適解から脱出する可能性を高めます。
• モーメンタムを使用した勾配降下法：過去の勾配の影響を考慮に入れ、鞍点を越えやすくします。
2. グローバル最適化アルゴリズム：
• シミュレーテッドアニーリング：高温からスタートして徐々に温度を下げることで、局所最適解から脱出しやすくします。
• 遺伝的アルゴリズム：複数の解候補を保持し、交叉や突然変異を通じて新たな解を探索します。
3. ベイズ最適化：
• 目的関数の確率モデルを構築し、そのモデルを用いて最適な探索点を効率的に決定します。
これは特に、評価にコストがかかる関数に対して効果的です。
3. オプティマイザの進化
機械学習の発展に伴い、特定のアーキテクチャや問題に特化した新しいオプティマイザが開発されています。LARS（Layer-wise Adaptive Rate Scaling）やLAMB（Layer-wise Adaptive Moments for Batch training）は、大規模なネットワークの効率的なトレーニングに重要な役割を果たしています。
LARS（Layer-wise Adaptive Rate Scaling）
LARSは、異なるレイヤーが異なる学習速度を持つ問題に対処するために開発されました。
このオプティマイザは、各レイヤーの重みのノルムとその勾配のノルムの比率を計算し、それに基づいて個々のレイヤーの学習率を調整します。
このアプローチにより、ネットワークの浅い部分と深い部分で異なるスケールの勾配が生じた場合でも、全体としての学習が均一に進行し、爆発的な勾配の問題を防ぎます。数学的には以下の式で表されます：
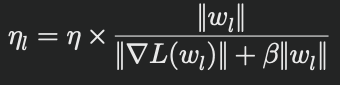
ここで、 ηlはレイヤーlの適応学習率、ηは基本学習率、wlはレイヤーlの重み、∇Lwlは損失関数に対するwlの勾配、βは安定性のための正則化パラメータです。
LAMB（Layer-wise Adaptive Moments for Batch training）
LAMBはLARSのアイデアを基に、アダムオプティマイザにモーメンタムと適応学習率の概念を組み合わせたものです。
この手法は特に大規模なデータセットとモデル、例えばGPTやBERTのようなトランスフォーマーベースのアーキテクチャで効果を発揮します。
LAMBは以下の更新式に従います：
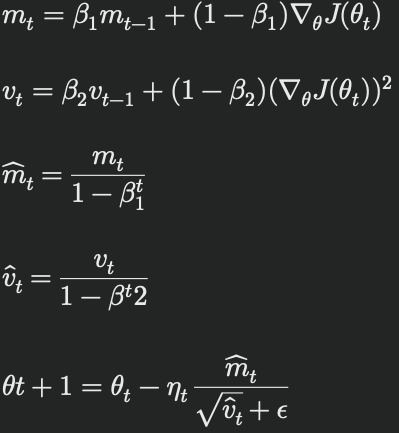
ここで、ηtはレイヤーごとに適応された学習率で、LARSと同様の手法で計算されます。
この更新法は、各パラメータに異なる重み付けを行うことで、学習プロセス全体の安定性と効
率を向上させます。
これらの進化したオプティマイザは、深層学習モデルのトレーニングにおける多くの実践的課題に対処するために設計されており、特に大規模なモデルや複雑なデータセットにおいて、その有効性が証明されています。
4. オプティマイザの未来
AI技術の進歩には、より効率的で強力なオプティマイザの開発が不可欠です。
次世代のオプティマイザは、以下の方向性で進化すると予想されています。
自動学習率調整
オプティマイザの効率を向上させるためには、学習率の選定と調整が鍵となります。
将来的には、学習プロセスを通じて自動で最適な学習率を見つけ出し、調整するオプティマイザが開発される可能性があります。
これにより、手動での微調整の必要性が低減し、より広範な問題に対しても適用可能な汎用的なモデルが実現可能になります。
メタラーニングとの組み合わせ
メタラーニング、または「学習するための学習」は、オプティマイザの設計に革命をもたらすかもしれません。
オプティマイザ自身が学習過程を通じて最適なアプローチを学習することで、特定のタスクやデータセットに最適化された学習戦略を自動生成することが期待されます。
フェデレーテッドラーニングへの適用
プライバシーを保護しつつ、分散データを利用するフェデレーテッドラーニングは、オプティマイザの新たな応用領域を提供します。
オプティマイザが各デバイスの局所的なデータに基づいて更新を行い、中央のサーバーで集約することで、プライバシーを損なうことなく全体のモデルを改善します。
5. まとめ
オプティマイザはAI開発の根幹に位置し、その進化はAIのパフォーマンスと応用範囲を直接的に拡大させます。
現在利用されている勾配降下法から確率的勾配降下法、さらにはアダムやLAMBのような高度な手法に至るまで、オプティマイザの進化は機械学習モデルの効率と効果を大幅に向上させてきました。
未来においても、オプティマイザの研究はAI技術の進化に欠かせない要素として、さらに高度なアルゴリズムの開発が進むことが期待されます。
これにより、AIはより複雑な問題を解決し、人間の生活をより豊かにするための新たな可能性を切り開いていくと筆者は感じています。
