1.はじめに
どうも、エンジニアのKです。
今回は、乗換案内やルート検索などに使用されている最短経路アルゴリズムについての記事を書いていこうと思います。
グラフ理論における最短経路問題とは、グラフ内の二つの頂点(またはノード)の間の経路を、構成エッジの重みの合計が最小になるように見つける問題です。
例えば、地図上で2つの交差点の間の最短ルートを探す場合、交差点を点、道路を線として考え、道路の長さを重さと見なして、その重さが最も少ないルートを見つけることを指します。
道路地図上の二つの交差点間の最短経路を見つける問題は、グラフ理論の最短経路問題の特殊なケースとしてモデル化することができます。
この場合、頂点は交差点に対応し、エッジは道路区間に対応し、それぞれのエッジには区間の長さが重みとして付けられます。
2.定義
頂点が共通のエッジに接続されているとき、それらの頂点は隣接しています。
無向グラフにおけるパスは、頂点のシーケンス
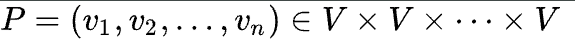
のように表され、頂点viはvi+1に隣接している場合に成り立ちます( 1 ≤ i < n )。
(ここでの vi は変数であり、それらの番号付けは列における位置に関連するもので、頂点の標準的なラベリングには関係しません。)
例えば、E = {ei, j}とするとき、E = {ei, j}は頂点 ( vi ) と ( vj ) に接続する辺を表します。
実数値の重み関数
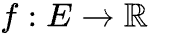
と無向(単純)グラフ ( G ) が与えられたとします。
ある頂点 ( v ) から別の頂点 ( v’ ) への最短経路とは、
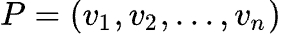
で表される経路(ここで ( v1 = v ) かつ ( vn = v’ ))であり、この経路はすべての可能な n の中で以下の和を最小化する経路になります:
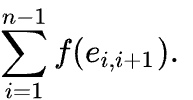
グラフ内の各エッジが単位重みを持つ場合、すなわち
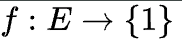
の場合、これは最小エッジ数の経路を見つけることと同等になります。
この問題は、以下のバリエーションと区別するために、単一対最短経路問題(single-pair shortest path problem)とも呼ばれます:
1. 単一始点最短経路問題(single-source shortest path problem): グラフ内のある始点頂点 v から他のすべての頂点への最短経路を見つける問題。
2. 単一終点最短経路問題(single-destination shortest path problem): 有向グラフ内のすべての頂点から特定の終点頂点 v への最短経路を見つける問題。これは、有向グラフ内の弧を逆にすることで単一始点最短経路問題に変換できます。
3. 全点対最短経路問題(all-pairs shortest path problem): グラフ内のすべての頂点対 v, v'間の最短経路を見つける問題。
3.アルゴリズム
この問題およびそのバリエーションを解くためのいくつかの有名なアルゴリズムが存在します。
• ダイクストラ法(Dijkstra’s algorithm): 非負のエッジ重みを持つ単一始点最短経路問題を解きます。
• ベルマン・フォード法(Bellman-Ford algorithm): エッジの重みが負の場合にも対応する単一始点最短経路問題を解きます。
• A探索アルゴリズム(A search algorithm): 単一対最短経路問題を解き、ヒューリスティクスを用いて探索を高速化します。
• フロイド・ワーシャル法(Floyd-Warshall algorithm): 全点対最短経路問題を解きます。
• ジョンソン法(Johnson’s algorithm): 全点対最短経路問題を解き、疎グラフ上ではフロイド・ワーシャル法よりも速い場合があります。
• ビタビ法(Viterbi algorithm): 各ノードに確率的重みを持つ最短確率経路問題を解きます。
4.応用例
最短経路アルゴリズムは、物理的な場所間の方向を自動的に見つけるために適用されます。
例えば、MapQuestやGoogle Mapsのようなウェブマッピングサイトの運転経路案内に使用されおり、この用途のために、特化した高速アルゴリズムが利用可能です。
日本ではYahooの乗換案内であったり、レストランでの自動運搬なども最短経路問題の良い例だと思います。
非決定性抽象機械を状態を記述する頂点と可能な遷移を記述するエッジで表現する場合、最短経路アルゴリズムは特定の目標状態に到達するための最適な選択のシーケンスを見つけるため、または与えられた状態に到達するのに必要な時間の下限を確立するために使用できます。
例えば、頂点がルービックキューブの状態を表し、各有向エッジが1回の動きや回転に対応する場合、最短経路アルゴリズムは可能な限り最少の手数で解くための解法を見つけるために使用します。
ネットワークや通信の観点から見ると、この最短経路問題はしばしば最小遅延経路問題(min-delay path problem)と呼ばれ、最広経路問題(widest path problem)と結びつけられることが多いです。例えば、アルゴリズムは最短(最小遅延)最広経路または最広最短(最小遅延)経路を探すことができます。
より気軽な応用例として、「six degrees of separation」というゲームがあります。
これは、映画に出演した俳優が同じ映画に出演した俳優を辿って最短経路を見つけるものです。
その他の応用例として、しばしばオペレーションズリサーチで研究されるものに、プラントや施設の配置、ロボティクス、交通、VLSI設計があります。
道路ネットワーク
道路ネットワークは、正の重みを持つグラフとして考えることができます。
ノードは道路の交差点を表し、グラフの各エッジは2つの交差点間の道路区間に対応します。エッジの重みは、その道路区間の長さ、区間を通過するのに必要な時間、または通過するためのコストに対応することがあります。
有向エッジを使用することで、一方通行の道路もモデル化可能です。
これらのグラフは、長距離移動の際にいくつかのエッジが他のエッジよりも重要であるという意味で特殊で(例:高速道路)、この特性は、ハイウェイ次元の概念を用いて形式化されています。
この特性を利用する多数のアルゴリズムが存在し、一般的なグラフよりもはるかに高速に最短経路を計算することができます。
これらのアルゴリズムはすべて2つのフェーズで動作します。
最初のフェーズでは、ソースノードやターゲットノードを知らずにグラフを前処理します。
第2のフェーズはクエリフェーズで、このフェーズではソースノードとターゲットノードが知られています。
このアイデアは、道路ネットワークが静的であるため、前処理フェーズは一度行えば同じ道路ネットワークに対する多くのクエリに使用できるというものです。
最も高速なクエリ時間を持つアルゴリズムはハブラベリング(hub labeling)と呼ばれ、ヨーロッパや米国の道路ネットワーク上の最短経路をマイクロ秒の一部で計算することができます。他に使用されている技術には次のようなものがあります:
• ALT(A*探索、ランドマーク、三角不等式)
• アークフラグ
• コントラクションヒエラルキー
• トランジットノードルーティング
• リーチベースプルーニング
• ラベリング
• ハブラベル
5.関連する問題
最短複数非連結経路(shortest multiple disconnected path)
最短複数非連結経路(shortest multiple disconnected path)は、レプテーション理論の枠組み内での原始経路ネットワークの表現で、最広経路問題(widest path problem)は、任意のエッジの最小ラベルができるだけ大きくなる経路を求める問題です。
制約付き経路問題
負のサイクルがないグラフでは最短経路問題は多項式時間で解けますが、望ましい経路に追加の制約がある最短経路問題は、制約付き最短経路問題(Constrained Shortest Path First)と呼ばれ、解決が難しくなります。
例えば、制約付き最短経路問題(constrained shortest path problem)は、経路の総コストを最小化しつつ、他のメトリックを指定の閾値以下に維持することを試みます。
これはNP完全問題であり(このような問題は大規模なデータセットに対して効率的に解けると信じられていません。*P = NP問題)、他のNP完全の例には特定の頂点集合を経路に含める必要がある問題があり、これは巡回セールスマン問題(TSP)に似ています。
TSPは、すべての頂点を正確に1回通過し、出発点に戻る最短経路を見つける問題です。
グラフの最長経路を見つける問題もNP完全です。
部分観測性
カナダ旅行者問題(Canadian traveller problem)や確率的最短経路問題(stochastic shortest path problem)は、グラフが移動者に完全には知られていなかったり、時間とともに変化したり、行動(移動)が確率的である場合の一般化です。
戦略的最短経路
場合によっては、グラフのエッジに「性格」があります。各エッジが自己の利益を持つ場合です。例えば、通信ネットワークでは、各エッジが異なる人に属する可能性があるコンピュータです。
異なるコンピュータは異なる伝送速度を持ち、ネットワーク内の各エッジの重みはメッセージの伝送にかかるミリ秒数に等しいです。
この問題の目標は、ネットワーク内の2点間でメッセージを最短時間で送信することです。
各コンピュータの伝送時間(各エッジの重み)がわかっていれば、標準の最短経路アルゴリズムを使用できます。
しかし、伝送時間がわからない場合、各コンピュータに伝送時間を教えてもらう必要がありますが、コンピュータは自己中心的で、伝送時間が非常に長いと嘘をついて、メッセージを送られないようにする可能性があります。
この問題の解決策として、VCGメカニズムの変種を使用して、コンピュータが真の重みを明らかにするインセンティブを与えることが考えられます。
負のサイクル検出
場合によっては、主な目標は最短経路を見つけることではなく、グラフに負のサイクルが含まれているかどうかを検出することです。いくつかの最短経路アルゴリズムはこの目的のために使用できます:
• ベルマン・フォードアルゴリズム(Bellman-Ford algorithm)は、負のサイクルを時間 O(|V||E|) で検出できます。
• CherkasskyとGoldbergは、負のサイクル検出のための他のいくつかのアルゴリズムを調査しています。6.一般代数フレームワークと半環に基づく最短経路問題
多くの問題は、経路に沿った加算と最小値を取る概念を適切に置き換えることで、最短経路の一形態として定式化できます。
これらの一般的なアプローチは、これらの2つの操作を半環(semiring)の操作とみなし、半環の乗法は経路に沿って行われ、加算は経路間で行われます。
この一般的なフレームワークは、代数的経路問題(algebraic path problem)として知られています。
ほとんどの古典的な最短経路アルゴリズム(および新しいアルゴリズム)は、このような代数構造上の線形システムを解くこととして定式化できます。
最近では、これらの問題(およびそれほど明らかに関連していない問題)を解決するための、さらに一般的なフレームワークが評価代数(valuation algebras)の名の下に開発されました。
7.確率的時間依存ネットワークにおける最短経路
現実の状況では、交通ネットワークは通常確率的であり、時間依存的です。
実際、旅行者が毎日同じリンクを移動する場合、旅行需要の変動(起点-終点マトリックス)だけでなく、工事区間、悪天候、事故、車両の故障などの事象により、異なる旅行時間になることがあります。
その結果、確率的時間依存(STD)ネットワークは、決定論的ネットワークよりも実際の道路ネットワークをより現実的に表現します。
過去10年間にわたるかなりの進展にもかかわらず、確率的道路ネットワークにおける最適経路をどのように定義し特定するかについては依然として議論の余地があります。
つまり、不確実性の下での最適経路の一意の定義はありません。
この質問に対する一つの可能で一般的な答えは、最小期待旅行時間の経路を見つけることです。
このアプローチの主な利点は、決定論的ネットワークのために導入された効率的な最短経路アルゴリズムを、確率的ネットワークにおける最小期待旅行時間の経路を特定するためにすぐに使用できることです。
しかし、このアプローチで特定された最適経路は信頼性に欠ける可能性があります。このアプローチは旅行時間の変動を考慮していないためです。
この問題に対処するために、一部の研究者は期待値の代わりに旅行時間の分布を使用し、動的プログラミングやダイクストラ法などの異なる最適化手法を使用して総旅行時間の確率分布を求めます。
これらの方法は、確率的なアーク長を持つネットワークにおける最短経路を見つけるために確率的動的プログラミングを使用します。
交通研究文献では、旅行時間の信頼性の概念は旅行時間の変動性と同義に使用されるため、一般的に旅行時間の変動が大きいほど信頼性が低くなると言えます。
旅行時間の信頼性をより正確に考慮するために、不確実性の下での最適経路の2つの一般的な代替定義が提案されています。
ある研究者は、所定の旅行時間予算内に到着する確率を最大化することを目指して、最も信頼性の高い経路の概念を導入しました。
また、他の研究者は、所定の到着確率を確保するために必要な旅行時間予算を最小化することを目的として、α-reliable path の概念を提唱しました。
8.まとめ
最短経路問題は、グラフ理論の重要な課題であり、多くの現実世界の応用に利用されています。
ただ、上記のようにさまざまな課題があるのも事実で、昨今のAI技術と同様に日々問題解決に向けたさまざまな研究がなされています。



