どうも、テンファイブ株式会社エンジニアのKです。
今回は数理最適化でもAI開発でも計算理論として度々使われる、多項式時間帰着についてテックブログにしてみました。
多項式時間帰着とは?
多項式時間帰着(polynomial-time reduction)は、計算理論において重要な概念の一つです。
ある問題 A を別の問題 B に多項式時間で変換できることを意味します。
これにより、もし B が多項式時間で解けるならば、問題 A も多項式時間で解けることが示されます。
具体的には、問題 A の任意のインスタンスを問題 B のインスタンスに多項式時間で変換する関数 f が存在する場合、問題 A は問題 B に多項式時間帰着可能と言います。
これを記号で A ≦pB と表します。
帰着のプロセス
1. 関数の定義: まず、多項式時間帰着では、問題 A の任意のインスタンスを取り、それを問題 B のインスタンスへと変換する関数 f を定義します。
この関数 f は多項式時間内で実行可能である必要があります。
つまり、入力のサイズに対して多項式のオーダーで時間が増加する程度で処理を完了させることが求められます。
2. 変換の保証: 関数 f によって生成された B のインスタンスが問題 B に対して正解された場合、その解を何らかの形で問題 A の解に変換できることが保証されていなければなりません。
この変換もまた、多項式時間内で行うことが必要です。
3. 解の対応性: 問題 A の解が存在する場合、その解を f に適用した結果、問題 B の解として有効である必要があります。
逆に、問題 B の解が問題 A の解に直接的に対応することも求められます。このように、解の間に一貫性が保たれることで、一方の問題の解法が他方の問題に適用可能であることを示します。
多項式時間とは?
多項式時間(polynomial time)とは、アルゴリズムが入力サイズ ( n ) に対して実行時間が多項式関数 ( P(n) ) で表される時間のことを指します。
ここで、多項式関数とは以下のような形式の関数です:
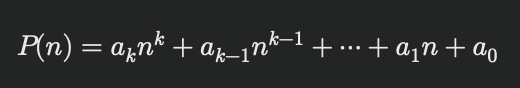
この関数の係数 ( a0, a1, ・・・・, ak ) は定数であり、( k ) は非負の整数です。
多項式時間アルゴリズムは、入力サイズが増加しても実行時間が急激に増加しないため、効率的とされます。
多項式時間の例
具体例として、以下のアルゴリズムの実行時間を考えてみます。
1. 線形検索(Linear Search):
• 入力サイズ ( n ) のリスト内で目標値を検索するアルゴリズム。
• 実行時間: ( O(n) )
2. バブルソート(Bubble Sort):
• 入力サイズ ( n ) のリストをソートするアルゴリズム。
• 実行時間: ( O(n^2) )
3. 二分探索(Binary Search):
• ソートされたリスト内で目標値を検索するアルゴリズム。
• 実行時間: ( O(log n) )
これらのアルゴリズムは全て、多項式時間アルゴリズムの例です。
特に、線形検索とバブルソートは入力サイズ ( n ) に対して多項式時間で実行されます。
多項式時間帰着の重要性
多項式時間帰着は、計算複雑性理論における多くの概念の基礎となっています。
特に、NP完全問題の定義において重要です。
NP完全問題は、全てのNP問題が多項式時間で帰着可能な問題として定義されます。
これにより、ある問題がNP完全であることを示すために、既知のNP完全問題にその問題が多項式時間で帰着可能であることを証明すれば良くなります。
NP完全問題とは?
NP完全問題(NP-complete problem)は計算理論、特に計算複雑性理論において、非常に重要なクラスの問題です。
これらの問題は理論的な研究だけでなく、実用的な観点からも重要な意味を持っています。
NP完全問題の定義
NP完全問題は、次の二つの条件を満たす問題の集合です:
1. NPに属する:問題の解が与えられたとき、その解が正しいかどうかを多項式時間内で検証できる問題です。
つまり、非決定的な計算モデルを使用した場合、その問題の解を多項式時間内で見つけることが可能です。
2. NP困難である(NP-hard):NPに属する全ての問題が多項式時間帰着可能な問題です。
これは、あらゆるNP問題が、その問題に対して多項式時間内で帰着できるということを意味します。
簡単に言えば、NP困難な問題は、NPに属するどの問題よりも難しい、または少なくとも同じくらい難しいとされます。
NP完全問題の特性
NP完全問題は、「もし一つのNP完全問題が多項式時間で解けるなら、全てのNP問題が多項式時間で解ける」という特性を持っています。
これは「P対NP問題」として知られる大きな未解決問題に直接関連しています。
P(多項式時間で解ける問題のクラス)がNP(多項式時間で検証可能な問題のクラス)に等しいかどうかは、現在でも解決されていない問題です。
NP完全問題の例
1. サティスファイアビリティ問題(SAT):
ブール論理式が与えられたときに、その論理式を真にする変数の割り当てが存在するかどうかを決定する問題です。
この問題は最初にNP完全であることが証明された問題であり、その他多くの問題がSATに多項式時間帰着されてNP完全性が示されています。
2. 巡回セールスマン問題(TSP):
与えられた都市とそれらを結ぶ経路のコストがわかっているときに、全ての都市を一度ずつ訪れて出発点に戻る最短ルートを見つける問題です。
3. クリーク問題:
与えられた無向グラフと整数 k に対して、k 個の頂点を持ち、それぞれの頂点が互いに隣接する完全部分グラフ(クリーク)が存在するかどうかを決定する問題です。
これらの問題は、その計算複雑性のために直接的な多項式時間解法が知られておらず、多くの場合、実際の応用において近似アルゴリズムやヒューリスティックな手法が用いられます。
また、これらの問題の研究は計算理論の進展に重要な寄与をしています。
応用例
多項式時間帰着は、アルゴリズム設計や計算複雑性の理論的研究において幅広く応用されています。以下にいくつかの応用例を紹介します。
1. アルゴリズムの設計:
問題 A を問題 B に帰着させることで、問題 B の効率的なアルゴリズムを利用して問題 A を解くことができます。
例えば、グラフの最大クリーク問題をグラフ彩色問題に帰着させることで、既存のグラフ彩色アルゴリズムを利用できます。
2. NP完全問題の同定:
新たに発見された問題がNP完全であることを示すために、既知のNP完全問題への多項式時間帰着を行います。
これにより、その問題が他のNP完全問題と同様に、効率的な解法が存在しない可能性が高いことが示されます。
3. 暗号理論:
暗号システムの安全性を示すために、多項式時間帰着が利用されます。
特定の計算問題の難しさを基にした暗号アルゴリズムは、その基礎となる問題が多項式時間で他の難しい問題に帰着可能であることを示すことで、アルゴリズムの安全性を保証します。
プログラムでの応用例
具体的なプログラムの世界での応用例としては、以下のようなものがあります。
1. アルゴリズムライブラリ:
多くのアルゴリズムライブラリは、多項式時間帰着の概念を利用して、異なる問題に対する一般的な解法を提供します。
例えば、SATソルバーは多くの論理問題をSAT問題に帰着させて解決します。
2. 問題解決ツール:
問題解決ツールでは、ユーザーが定義した問題を内部的に標準的な問題に帰着させ、その解法を提供することが一般的です。
これにより、ユーザーは特定の問題に対して効率的な解法を容易に利用できます。
3. データベース最適化:
データベースクエリの最適化においても、クエリを他の形式に変換することで効率的な実行計画を立てることができます。
多項式時間帰着の概念は、複雑なクエリを簡略化し、より効率的に処理するために利用されます。
まとめ
多項式時間帰着は、計算理論とアルゴリズム設計における基本的な概念です。その応用は理論的な研究から実際のプログラム設計まで多岐にわたります。この概念を理解することで、複雑な問題を効率的に解決するための新たなアプローチを見出すことができます。