どうもエンジニアのKです。
私たちの日常は、無数の選択肢と決断で満ちています。何を食べるか、どのルートで通勤するか、どの商品を買うか…これら全てが、ある意味で最適化の問題です。
しかし、これらの日常的な決断をより科学的にアプローチする方法があります。
それが「線形最適化」という数学的手法です。
ということで今回は、線形最適化の基本とその驚くべき日常生活への応用について掘り下げていきます。
ビジネスや工学だけでなく、私たちの身近な問題解決にも役立つこの技術を通じて、より良い選択を行うための考え方を紹介します。
線形最適化の基本
線形最適化(または線形計画法)は、一連の線形関係式によって表される制約条件を満たしつつ、線形の目的関数を最大化または最小化する問題を解く数学的手法です。
線形最適化の数学的定式化
線形最適化の問題は一般的に次の形式で表されます:
目的関数
線形最適化問題の目的は、目的関数を最大化または最小化することです。
目的関数は次のように表されます:
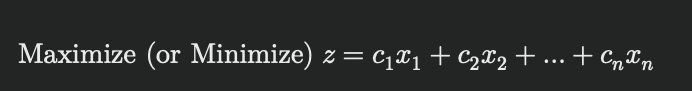
制約条件
制約条件は、変数 (xi) が満たすべき一連の線形方程式です。
これらの制約は通常、不等式で表されます:
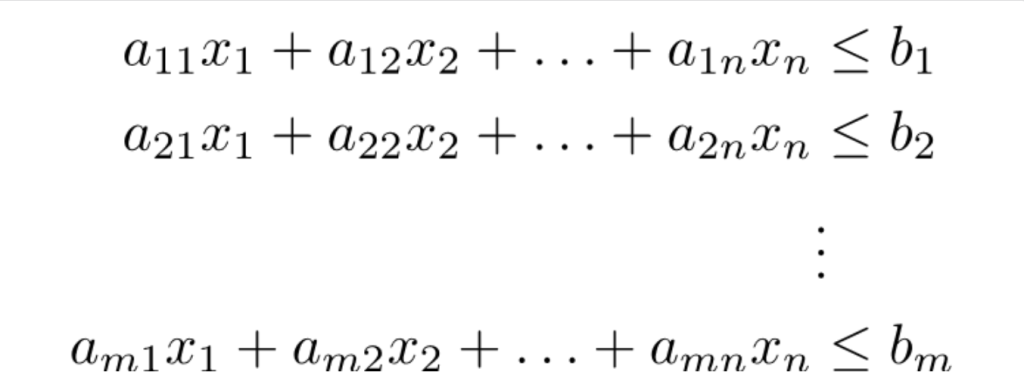
変数の非負条件
線形最適化問題において、変数 x_i は非負の値を取る必要があります。
この条件は以下のように表されます:
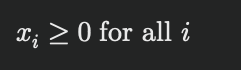
事例: スーパーマーケットでの最適な買い物計画
問題設定
スーパーマーケットでの買い物では、消費者は限られた予算の中で、最も満足度が高い商品を選びたいと考えます。
この問題は、特に健康的な食事を意識している場合、栄養価の高い商品を選びながら総カロリーを管理することが必要です。
線形最適化を利用すれば、これらの要素を数学的にモデル化し、最適な買い物リストを生成することが可能になります。
モデルの構築
目的関数
目的関数は、購入する商品の総満足度を最大化することです。
ここで、「満足度」とは商品ごとに割り当てられた価値であり、これは栄養価、好み、価格など複数の要因に基づいて決定されます。
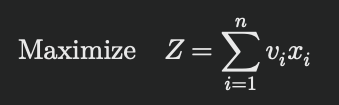
ここで、( vi ) は商品 ( i ) の満足度スコア、( xi ) は商品 ( i ) の購入量を表します。
制約条件
• 予算制約: 合計支出が予算 ( B ) を超えないようにします。
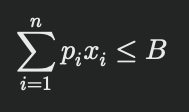
ここで、( pi ) は商品 ( i ) の価格です。
• 栄養制約: 特定の栄養素(例えばタンパク質、ビタミン等)の合計摂取量が推奨範囲内に収まるようにします。
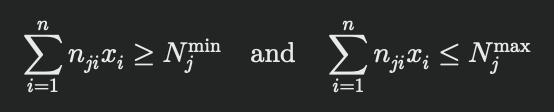
ここで、( n{ji} ) は商品 ( i ) の栄養素 ( j ) の含有量、( N_j^min) と ( N_j^max) は栄養素 ( j ) の推奨最小/最大摂取量です。
• 購入量制限: 各商品は最小単位 ( li ) から最大単位 ui まで購入可能です。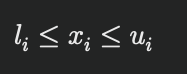
このモデルを設定した後、線形計画法を用いて最適解を求めます。具体的には、シンプレックス法や内点法などのソルバーを使用して、制約条件を満たしつつ目的関数を最大化する商品の組み合わせを見つけ出します。この解析により、消費者は予算内で最も満足度の高い買い物を効率的に計画できるようになります。
このように線形最適化は、具体的な制約と目的に基づいて最適な選択を支援する強力なツールとして、日常生活における複雑な意思決定プロセスを助けることができます。
日常生活への応用
線形最適化のこのような応用は、私たちの日常生活における意思決定に科学的なアプローチを提供してくれます。
具体的には、以下のような利点があります。
予算と健康の同時管理
計画的な買い物を行うことで、予算を守りながら健康的な食生活を送ることが可能になります。
これは特に、限られた予算の中で最大限の健康効果を得るための戦略を立てる際に有効です。
時間の節約
何を買うか事前に計画することで、スーパーマーケットでの買い物時間を大幅に短縮できます。
無駄遣いの削減
必要なものだけを計画的に購入することで、衝動買いや不必要な商品の購入を減らし、節約につながります。
最後に
この記事を通じて、線形最適化がいかに私たちの日常の選択に科学的な根拠を提供し、より賢い消費行動を支援するかが理解できたかと思います。
予算管理、健康維持、時間節約の観点からも、線形最適化は私たちの生活に欠かせないツールです。
これを利用することで、日々の決断がより合理的で効率的になり、最終的には賢明な選択と持続可能な生活スタイルを実現できます。
次回の買い物でこの方法を試してみてはいかがでしょうか?
理論が現実の行動に変わる瞬間を、ぜひ体験してみてください。